데이터링크층의 주 역할 중 하나인 오류 제어는 크게 2 가지 오류 검출과 오류 정정으로 나뉜다.
일반적으로 오류 검출이 오류 정정보다 휠씬 쉽기 때문에 특수한 경우가 아닌 이상 오류 정정은 잘 하지 않는다. 워낙 네트워크 성능이 좋아졌기 때문에 오류 정정할 시간에 그냥 오류 검출 후 재전송 하는 게 더 빠르다..
그래서 크게 오류 제어는 3가지 기법으로 나눠진다.
1. 블록 부호화 (Block-encoding)
2. 순환 중복 검사 (CRC)
3. 검사합 (CheckSum)
오류의 유형에는 단일 비트 오류와 폭주 비트 오류가 있다. 말 그대로 단일 비트는 데이터 단위 중 오직 하나의 비트만 바뀌는 것을 의미한다.
폭주 비트 오류는 2개 이상의 연속된 비트가 바뀌는 것을 의미한다. 이런 오류를 검출하거나 정정하기 위해 데이터 단위에 추가적으로 붙이는 비트를 Redundancy 라고 한다.
블록 부호화
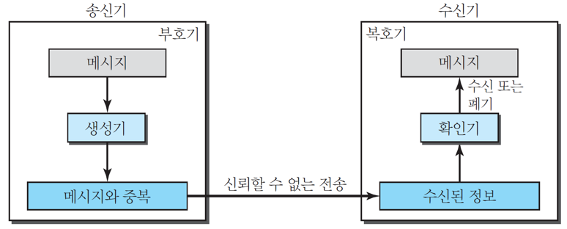
이렇게 메시지가 있을 때 생성기와 확인기를 통해 신뢰할 수 없는 전송이 왔을 때 검증하는 원리이다.
하지만 이 방법은 2개 이상의 연속된 비트가 고장나는 폭주 비트 오류를 잡을 수 없다.
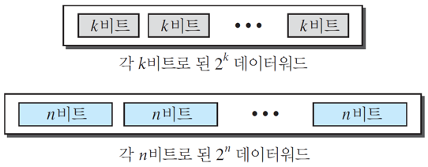
블록 부호화에서는 메시지를 데이터워드(data word)라고 하는 k비트의 블록으로 나눈다. 그리고 각 블록에서 redundancy를 r 만큼 더해 n = k + r 이 되게끔 새로운 블록을 만든다. 그리고 이 n 비트의 블록들을 모아놓은 것을 코드워드(code word)라고 부른다.
이 때 폭주 비트를 잡을 수 없는 이유를 예제로 설명하자면
n = 3, k = 2 일 때 다음과 같은 데이터워드와 코드워드가 있다.

01을 011로 부호화 했다고 가정하자.
1. 수신자가 011을 수신한다. 코드워드에 011이 존재하므로 오류가 나지 않았다고 판단해 대응하는 데이터워드 01을 추출한다.
2. 코드워드가 전송되던 중 비트 하나가 손상되어 111이 되었다. 111은 코드워드에 존재하지 않으므로 버려진다.
3. 비트 2개가 손상되어 000이 되었다. 그런데 000은 유효한 코드워드이므로 받아드려져 00을 추출한다.
이렇듯 연속으로 2개의 비트가 잘못될 시 올바르게 오류제어를 할 수 없는 모습이다.
어떻게 해결할 것인가?
해밍 거리
오류 제어를 위한 중심 개념 중 하나인 해밍 거리는 같은 크기의 두 워드 x,y 사이의 거리를 d(x,y) 로 나타내는 것을 말한다.
해밍 거리는 두 비트를 XOR 연산한 결과의 1의 개수이다.
예를 들어 d(000,111) = 3 이다. 000 ^ 111 = 111 이기 때문에 1이 3개라 3이 된다.
오류검출을 위한 최소 해밍 거리는 가능한 모든 코드워드 쌍의 해밍거리 중 최소 이다.
패리티 검사 코드
패리티 검사 코드는 홀수 개의 오류를 검출할 수 있다.
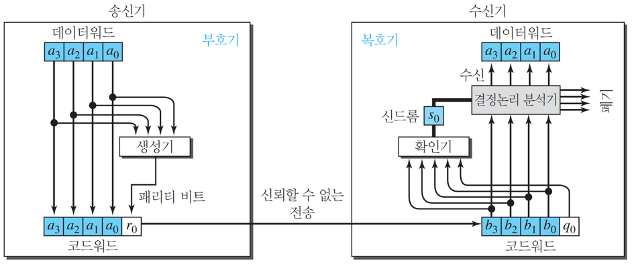
패리티 비트는 생성기를 통해 데이터 워드 중 하나의 비트만 코드워드에 추가한다.
추가하는 규칙은 다음과 같다.
- 데이터워드의 1의 개수가 홀수면 1
- 데이터워드의 1의 개수가 짝수면 0
이렇게 만들어진 코드워드는 반드시 1의 개수가 짝수며, 손상되었을 때 짝수가 아니면 오류가 발생한 것으로 본다.

그래서 1,3,5번 같이 1의 개수가 홀수인 코드워드가 수신될 시 , 오류로 판단해 버리는 것이다.
아스키코드가 7 비트인 이유도 이 패리티비트를 하나 붙여 8비트 = 1 바이트로 만들기 위함이다.
이 패리티 비트 방식을 더욱 좋게 바꾼 것이 2차원 패리티 검사이다.
패리티 비트를 추가하는 규칙을 하나의 코드워드가 아닌 여러개의 코드워드에 동시에 적용해 행과 열에 대한 모든 패리티 비트를 검사하는 것이다.

하지만 이것 역시 4개의 오류가 저렇게 행과 열에 정확히 걸려버리면 알아낼 방법이 없다.
순환 중복 검사(CRC, Cyclic Redundancy Check)
순환 중복 검사란 순환 코드를 이용한 방식이다. 순환 코드는 하나의 특별한 성질을 갖는 선형 블록으로 순환 코드에서 코드워드를 순환시키면 다른 코드워드를 얻는 성질이다. 이것은 나머지 연산과 유사하며, CRC는 이 선형적인고 순환적인 성질을 만족한다.
앞서 배운 패리티 비트는 데이터 워드의 1의 개수로 코드워드를 만들었다.
그렇다면 CRC에서는 어떤 규칙을 통해 코드워드를 만들어 낼까?
바로 데이터워드를 어떤 다항식으로 나눠서 나온 나머지를 코드워드에 붙인다.
무슨 말이냐?

여기 제수라고 하는 공통된 $d3 d2 d1 d0$가 앞서 말한 어떤 다항식이다. 공통된 제수가 있고 데이터워드를 제수로 나눈다. 나눌 때 마다 뒤에 n - k 개의 0을 덧붙이며 마지막에 생긴 나머지가 코드워드를 생성하는 비트가 된다.

여기선 제수로 1011이 선택되었다. 그리고 1001 이라는 데이터워드를 코드워드로 변환하는 과정을 설명한 그림이다.
몫의 가장 왼쪽부터 1 * 1011 = 1011 이기 때문에 가장 왼쪽엔 1이 온다. 몫을 사용하지는 않지만 정상적인 나눗셈이 되려면 필수다.
그렇게 생긴 1011은 1001과 빼기 연산이 일어난다. 즉, 저 나눗셈의 과정을 순서대로 표현하자면 곱하기는 AND(&), 빼기는 XOR(^)로 나타냈을 때
1. 1011 & 1 = 1011 (1001의 LSB가 1 이기 때문에)
2. 1001 ^ 1011 = 0110
3. 1011 & 0 = 0000 ( 0100의 LSB가 0 이기 때문에 )
4. 0100 ^ 0000 = 1000
5. 1011 ^ 1 = 1011 (1011의 LSB가 1 이기 때문에)
6. 1000 ^ 1011 = 0110
7. 1011 & 0 = 0000 (0110의 LSB가 0 이기 때문에)
8. 0110 ^ 0000 = 110
나머지 3 자리 비트인 110이 데이터워드 1001의 코드워드 뒤에 들어가는 비트가 된다.
그래서 코드워드는 [1001 | 110] 가 된다.
꼭 이렇게 이진수로 하지 않고 다항식으로도 할 수 있다. 애초에 비트가 2^k 의 합으로 정수를 나타낼 수 있기 때문에.. 근데 난 비트가 편해서 그냥 이렇게 계산하는걸 선호한다.

뭐 이렇게 나타낼 수 있다. 그리고 계산하는 방법은 똑같다.
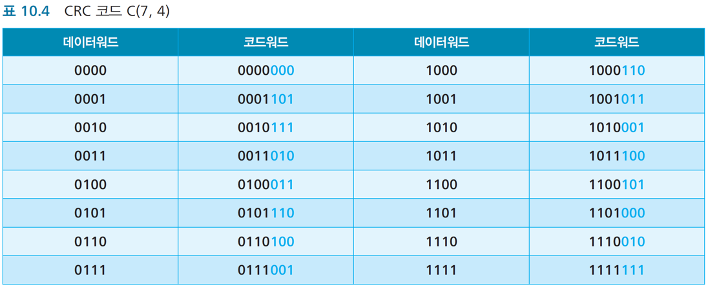
그럼 여기서 드는 의문은 계산하는 법은 알겠는데, 제일 처음 지정한 공통된 제수 1011 은 어디서 가져온 거냐? 인데 이건 바로 "미리 사람들이 지정해 놨다." 가 정답이다.

LAN 에서 사용하는 CRC-32가 가장 대표적으로 알려진 표준이며 공통된 제수는 이 표를 따른다. 앞서 설명한 1011은 그냥 설명을 쉽게 하기 위해 만든 것이다.
순환 중복 검사 (CRC) 방식의 장점은 크게 3가지로
1. 단일 비트, 두 비트, 홀수 비트 및 폭주 비트 모두 검출 가능
2. 하드웨어나 소프트웨어로 쉽게 구현 가능
3. 하드웨어로 구현 시 빠른 속도 보장
이다.
검사합(CheckSum)
모든 길이의 메시지에 적용시킬 수 있는 오류 검출 기법이다. 검사합은 보통 데이터링크층 보다는 네트워크층과 전송층에서 사용된다.
마찬가지로 생성기와 검사기가 존재하며 맨 마지막 블록에 검사합을 합쳐서 보낸다.
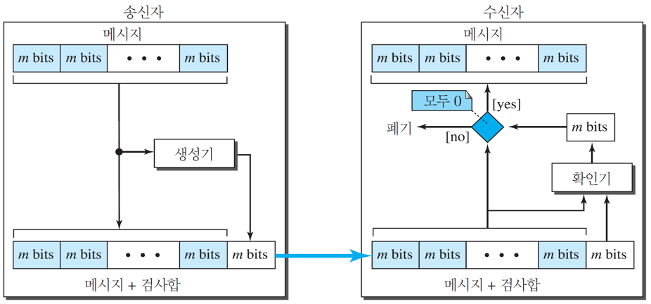
그래서 모든 메시지에 검사합을 확인해 모두 0이 나오면 변조되지 않았다고 판단하고 그렇지 않으면 폐기하는 간단한 방식이다.
1의 보수 방식을 사용하며 구체적으로는 다음과 같이 동작한다.

36을 2진수로 바꾸면 100100이다. 이때 오른쪽 4비트와 나머지 왼쪽비트를 더해서 검사합을 만든다.

그리고 그걸 다시 1의 보수를 취해 1001 (9) 라는 값을 구한다. 그리고 맨 마지막에 9를 붙여서 보낸다.
검사할 때는 다 합친 후 45가 나오고, 똑같이 4비트로 표현해 15를 도출하면 1111 이므로 1의 보수가 0인 모습이 보인다.
그럼 변조되지 않았다고 판단하는 방식이다.
그러나 이 방식은 데이터 손실이 취약한 물리 계층에서 어떤 손상이 일어날지 모르므로 워드의 값이 증가한 만큼 다른 워드의 값이 감소해서 우연히 합이 일치할 가능성이 있다. 2차원 패리티도 우연히 4개가 같은 행과 열에 있으면 잡지 못하는데 이건 오죽할까 싶다.
그래서 데이터링크층에서의 오류 검출은 CRC가 대표적인 방식이다.
정리
- 패리티 검사 : 홀수개의 오류만 검출 가능, 개선된 더블 패리티 방식도 있지만 그것도 행과 열 같은 자리에 4개의 오류 발생 시 검출 불가
- CRC : 거의 모든 오류 검출 가능, 강력한 오류 검출 성능, 표준으로 CRC-32는 LAN에서 씀
- 검사합 : 데이터링크층에서는 잘 안씀, 폭주 비트 잡을 순 있음 데이터 워드의 합으로 구하는 거라서 연속된 데이터가 잘못되더라도 합이 다르면 검출할 수 있음 근데 우연히 감소된 만큼 똑같이 증가해서 결론적으로 합이 같아지면 못찾음
등장한 약어
CRC : Circuit Redundancy Check - 순환 중복 검사
'network' 카테고리의 다른 글
| [데이터 통신] Chapter 08 교환 연습 문제 & 정답 (0) | 2023.06.13 |
|---|---|
| [데이터 통신] Chapter 12 매체 접근 제어 (MAC) (1) | 2023.06.12 |
| [데이터 통신] Chapter 11 데이터 링크 제어 DLC (0) | 2023.06.11 |
| [데이터 통신] Chapter 09 데이터 링크층 개요 (0) | 2023.06.11 |
| [데이터 통신] Chapter 08 교환 - 다양한 교환망 (0) | 2023.06.11 |



